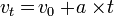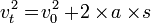Kecepatan adalah besaran vektor yang menunjukkan seberapa cepat benda berpindah. Besar dari vektor ini disebut dengan kelajuan dan dinyatakan dalam satuan meter per sekon (m/s atau ms⁻¹).

Kecepatan biasa digunakan untuk merujuk pada kecepatan sesaat yang didefinisikan secara matematis sebagai:

\mathbf {v} =\lim _{\Delta t\to 0}{{\mathbf {r} (t+\Delta t)-\mathbf {r} (t)} \over \Delta t}={\operatorname {d} \mathbf {r}  \over \operatorname {d} t}

di mana

\mathbf {v}

adalah kecepatan sesaat dan

\mathbf {r} (t)

adalah perpindahan fungsi waktu.

Selain kecepatan sesaat, dikenal juga besaran kecepatan rata-rata

{\bar {\mathbf {v} }}

yang didefinisikan dalam rentang waktu

\Delta t\,

yang tidak mendekati nol.

{\bar {\mathbf {v} }}={\frac {\Delta \mathbf {r} }{\Delta t}}

Satuan kecepatan

Beberapa satuan kecepatan lainnya adalah:

meter per detik dengan simbol m/s
kilometer per jam dengan simbol km/jam atau kph
mil per jam dengan simbol mil/jam atau mph
knot merupakan singkatan dari nautical mile per jam
Mach yang diambil dari kecepatan suara. Mach 1 adalah kecepatan suara.
Kecepatan cahaya atau disebut juga sebagai konstanta cahaya dinyatakan dengan simbol c adalah:

c=299,792,458\ m/s

Perubahan kecepatan tiap satuan waktu dikenal sebagai percepatan atau akselerasi.

Contoh berbagai kecepatan

Berikut disampaikan kecepatan dari yang paling rendah ke tercepat:

Kecepatan siput = 0.001 ms⁻¹; 0.0036 km/h; 0.0023 mph.
Jalan cepat = 1.667 ms⁻¹; 6 km/h; 3.75 mph.
Olympic sprinters (rata-rata dalam 100 meter) = 10 ms⁻¹; 36 km/h; 22.5 mph.
Batas kecepatan di jalan bebas hambatan Perancis = 36.111 ms⁻¹; 130 km/h; 80 mph.
Kecepatan puncak pesawat Boeing 747-8 = 290.947 ms⁻¹; 1047.41 km/h; 650.83 mph; (officially Mach 0.85)
Rekor kecepatan pesawat = 980.278 ms⁻¹; 3,529 km/h; 2,188 mph.
Space shuttle pada saat masuk orbit bumi = 7,777.778 ms⁻¹; 28,000 km/h; 17,500 mph.
Kecepatan suara di udara (Mach 1) adalah 340 ms⁻¹, dan 1500 ms⁻¹ di air

A. Kecepatan Sesaat

Kecepatan didefinisikan sebagai laju suatu benda dalam arah tertentu. Dalam banyak situasi, untuk mencari kecepatan, kita bisa menggunakan persamaan v = s/t, di mana v sama dengan kecepatan, s sama dengan jarak total perpindahan benda dari posisi awalnya, dan t sama dengan waktu. Tetapi, cara ini hanya memberikan nilai kecapatan "rata-rata" dari benda tersebut sepanjang perpindahannya. Dengan menggunakan kalkulus, Anda bisa menghitung kecepatan benda pada titik manapun sepanjang perpindahannya. Nilai ini disebut dengan "kecepatan sesaat" dan dapat dihitung dengan persamaan v = (ds)/(dt), atau, dengan kata lain, adalah turunan dari persamaan kecepatan rata-rata benda.

cara menghitung kecepatan sesaat

1
Mulai dengan persamaan kecepatan perpindahan benda. Untuk mendapatkan nilai kecepatan sesaat suatu benda, pertama-tama kita harus memiliki persamaan yang menjelaskan posisinya (dalam hal perpindahannya) pada titik waktu tertentu. Hal ini berarti persamaan itu harus memiliki variabel s (yang berdiri sendiri) di salah satu sisinya, dan t di sisi lainnya (namun tidak harus berdiri sendiri), seperti ini:

s = -1.5t² + 10t + 4
- Dalam persamaan tersebut, variabelnya adalah:
  
  Perpindahan = s . Yaitu jarak yang ditempuh benda dari titik awalnya. Sebagai contohnya, jika suatu objek menempuh jarak 10 meter ke depan dan 7 meter ke belakang, maka jarak tempuh totalnya adalah 10 - 7 = 3 meter (bukan 10 + 7 = 17 meter).
  Waktu = t . Variabel ini sudah cukup jelas. Biasanya dinyatakan dalam satuan detik. #Ambil turunan persamaan tersebur. Turunan suatu persamaan adalah persamaan lain yang dapat memberikan nilai slope dari titik tertentu. Untuk mencari turunan rumus perpindahan benda, turunkan fungsinya dengan aturan umum berikut ini: Jika y = a*xⁿ, Turunan = a*n*x^n-1. Aturan ini berlaku untuk setiap komponen yang berada dalam sisi "t" dalam persamaan.
- Dengan kata lain, mulailah dengan menurunkan sisi "t" dalam persamaan dari kiri ke kanan. Setiap kali Anda mencapai nilai "t", kurangi 1 dari nilai eksponen dan kalikan seluruhnya dengan eksponen awal. Konstanta apapun (variabel yang tidak mengandung "t") akan hilang karena dikalikan dengan 0. Proses ini tidak sesulit yang dibayangkan, ayo turunkan persamaan dalam langkah di atas seperti contoh:
  
  s = -1.5t² + 10t + 4
  (2)-1.5t^(2-1) + (1)10t^{1 - 1} + (0)4t⁰
  -3t¹ + 10t⁰
  -3t + 10
2
Ganti variabel "s" dengan "ds/dt." Untuk menunjukkan bahwa persamaan baru Anda adalah turunan persamaan sebelumnya, ganti "s" menjadi "ds/dt". Secara teknis, notasi ini berarti "turunan s terhadap t." Cara yang lebih sederhana untuk memahaminya adalah bahwa ds/dt adalah nilai kemiringan (slope) pada titik manapun dalam persamaan pertama. Sebagai contohnya, untuk menentukan slope dari garis yang dibuat dari persamaan s = -1.5t² + 10t + 4 at t = 5, kita dapat memasukkan nilai "5" ke dalam persamaan turunannya.
- Dalam contoh yang digunakan, persamaan turunan pertama akan tampak seperti ini sekarang:
  
  ds/dt = -3t + 10
3

Masukkan nilai t ke dalam persamaan yang baru untuk mendapatkan nilai kecepatan sesaat. Sekarang setelah Anda memiliki persamaan turunan, mencari kecepatan sesaat pada titik manapun akan mudah dilakukan. Yang perlu Anda lakukan adaah memilih nilai t dan memasukkannya ke dalam persamaan turunan Anda. Sebagai contohnya, jika Anda ingin mencari kecepatan sesaat pada t = 5, Anda bisa mengganti nilai t dengan "5" dalam persamaan turunan ds/dt = -3 + 10. Kemudian menyelesaikan persamaannya seperti ini:

ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 meter/second

Perhatikan bahwa satuan yang digunakan di atas adalah "meter/second". Karena yang kita menghitung perpindahan dalam meter dan waktu dalam detik (second) dan kecepatan secara umum adalah perpindahan dalam waktu tertentu, maka satuan ini sudah tepat untuk digunakan.

2. Kecepatan Rata-Rata

Pengertian Kecepatan Rata-Rata
Kecepatan rata-rata adalah jarak perjalanan rata-rata yang ditempuh setiap satuan waktu. Sebuah mobil yang menumpuh jarak misalnya 100 kilometer pasti pernah berjalan pelan misalnya saat melewati jalan rusak, tikungan, jalan sempit, dan lain lain. Mobil itu juga mungkin sempat berhenti beberapa kali karena menjumpai lampu merah menyala di persimpangan jalan, mengisi bahan bakar, macet, dan lain sebagainya. Kecepatan mobil tersebut pada waktu tertentu disebut kecepatan sesaat yang ditunjukkan oleh panel speedometer di dashboard mobil.

Satuan Kecepatan dalam Sistem Metrik

Satuan kecepatan dalam sistem metrik (sistem internasional, SI) yang paling umum adalah meter/detik (m/detik) dan kilometer/jam (km/jam).

Rumus Menghitung Kecepatan Rata-Rata
Untuk menghitung kecepatan rata-rata perjalanan atau pergerakan suatu benda, maka harus diketahui jarak tempuh dan waktu tempuh. Kecepatan rata-rata pergerakan sebuah benda merupakan hasil pembagian besaran jarak dengan besaran waktu tempuh. Rumus menghitung jarak rata-rata berdasarkan jarak tempuh dan waktu tempuh adalah sebagai berikut.

Contoh Cara Menghitung Kecepatan Rata-Rata
Contoh 1
Soal: Seorang pelari atletik dapat menempuh jarak 200 meter dalam waktu 25 detik. Berapa kecepatan rata-rata pelari atletik tersebut? (Petunjuk: kecepatan rata-rata = jarak tempuh/waktu tempuh).
Jawab:
Jarak tempuh = 200 m
Waktu tempuh =25 detik
Kecepatan rata-rata = 200/25 = 8 m/detik.

Contoh 2
Soal: Sebuah mobil menempuh jarak 110 kilometer dalam waktu 2 jam. Hitunglah kecepatan rata-rata mobil tersebut. (Petunjuk: kecepatan rata-rata = jarak tempuh/waktu tempuh).
Jawab:
Jarak tempuh = 110 km
Waktu tempuh =2 jam
Kecepatan rata-rata = 110/2 = 55 km/jam.

Contoh 3

Soal: Sebuah mobil berjalan dari kota A ke kota B yang jaraknya 50 km dalam waktu 1 jam. Mobil itu melanjutkan perjalanan ke kota C yang berjarak 90 km dari kota B dalam waktu 2 jam. Dari kota C mobil itu melanjutkan perjalanan ke kota D yang jaraknya 40 km dalam waktu 1 jam.Hitung kecepatan rata-rata mobil tersebut dari kota A ke kota D. (Petunjuk: kecepatan rata-rata = jarak tempuh/waktu tempuh).

Jawab:

Jarak tempuh = 50 + 90 + 40 = 180 km

Waktu tempuh = 1 + 2 + 1 = 4 jam

Kecepatan rata-rata = 180/4 = 45 km/jam.

Konsep Turunan (Diferensial) dan integral

Konsep Turunan dan integral pada vektor posisi, kecepatan dan percepatan

Diketahui bahwa kecepatan merupakan turunan dari posisi, maka jika kecepatan diintegralkan akan menghasilkan posisi. Percepatan merupakan turunan dari kecepatan maka jika percepatan diintegralkan akan menghasilkan kecepata. Secara ringkas dapat digambarkan dengan :

Contoh 1 :

Contoh 2 :

3. Percepatan

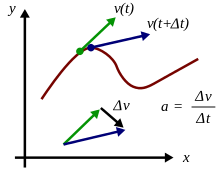
Dalam fisika, percepatan atau akselerasi adalah perubahan kecepatan dalam satuan waktu tertentu. Akselerasi sebuah objek disebabkan karena gaya yang bekerja pada objek tersebut, seperti yang dijelaskan dalam Hukum kedua Newton.^[1] Satuan SI untuk akselerasi adalah meter per sekon kuadrat (m s⁻²). Percepatan adalah besaran vektor, sehingga percepatan memiliki besaran dan arah.^[2]^[3] Sebagai vektor, total gaya sama dengan hasil kali massa objek (besaran skalar) dan percepatannya. Umumnya, percepatan dilihat sebagai gerakan suatu objek yang semakin cepat ataupun lambat. Dengan kata lain, objek yang membelok (misalnya mobil yang sedang menikung)-pun memiliki percepatan juga.

Percepatan adalah perubahan kecepatan per satuan waktu

Definisi dan sifat-sifat

Besaran kinematis pada partikel klasik: massa m, posisi r, kecepatan v, percepatan a.

Percepatan rata-rata

Akselerasi adalah perubahan kecepatan. Pada titik manapun pada lintasan, besaran percepatan sama dengan perubahan kecepatan pada besaran dan arah pada titik tersebut. Akselerasi sebenarnya pada waktu tadalah limit sebagai interval waktu Δt→ 0 dari Δv/Δt

Percepatan rata-rata suatu objek untuk tiap waktu adalah perubahan kecepatan

(\Delta \mathbf {v} )

dibagi waktu

(\Delta t)

. Secara matematis,

\mathbf {\bar {a}} ={\frac {\Delta \mathbf {v} }{\Delta t}}.

Percepatan sesaat

Percepatan sesaat, adalah limit dari percepatan rata-rata per interval waktu yang sangat kecil. Dalam kalculus, percepatan sesaat adalah turunan vektor kecepatan terhadap waktu:

\mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}

(Disini dan dimanapun, jika gerak berada dalam garis lurus, besaran vektor dapat digantikan dengan skalar dalam persamaan.)

Dapat dilihat bahwa integral fungsi akselerasi

a (t)

adalah fungsi kecepatan

v (t)

; dimana luasan di bawah kurva akselerasi vs waktu (

a

vs.

t

) sama dengan kecepatan.

\mathbf {v} =\int \mathbf {a} \ dt

Karena akselerasi didefinisikan sebagai turunan kecepatan

v

terhadap waktu

t

dan kecepatan didefinisikan sebagai turunan posisi

x

terhadap waktu, maka akselerasi adalah turunan kedua dari

x

terhadap

t

:

\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {x} }{dt^{2}}}

Dalam mekanika klasik, percepatan suatu objek bermassa tetap berbanding lurus dengan resultan gaya yang bekerja padanya dan berbanding terbalik dengan massanya.

\mathbf {F} =m\mathbf {a} \quad \to \quad \mathbf {a} =\mathbf {F} /m

dengan F adalah gaya yang bekerja pada objek, m adalah massa objek, dan a adalah percepatan pusat massa benda. Ketika kecepatan semakin mendekati kecepatan cahaya, efek relativistik menjadi semakin besar.

Percepatan bisa bernilai positif dan negatif. Bila nilai percepatan positif, hal ini menunjukkan bahwa kecepatan benda yang mengalami percepatan positif ini bertambah (dipercepat). Sebaliknya bila negatif, hal ini menunjukkan bahwa kecepatan benda menurun (diperlambat). Contoh percepatan positif adalah: jatuhnya buah dari pohonnya yang dipengaruhi oleh gravitasi. Sedangkan contoh percepatan negatif adalah: proses pengereman mobil.

Dari bawah ke atas:

Fungsi akselerasi a(t);
Integral dari akselerasi adalah fungsi kecepatan v(t);
Integral dari kecepatan adalah fungsi posisi s(t).

Rumus GLB dan GLBB

Gerak lurus beraturan

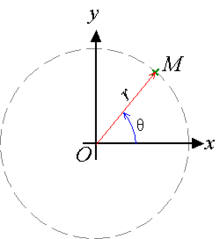
Sistem koordinat kutub dua dimensi

Gerak Lurus Beraturan (GLB) adalah suatu gerak lurus yang mempunyai kecepatan konstan. Maka nilai percepatannya adalah a = 0. Gerakan GLB berbentuk linear dan nilai kecepatannya adalah hasil bagi jarak dengan waktu yang ditempuh.

Rumus:

$\!v=\frac{s}{t}$

Dengan ketentuan:

$\!s$ = Jarak yang ditempuh (km, m)
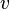$\!v$ = Kecepatan (km/jam, m/s)
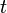$\!t$ = Waktu tempuh (jam, sekon)

Catatan:

Untuk mencari jarak yang ditempuh, rumusnya adalah $\!s=\!v\times\!t$ .
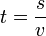Untuk mencari waktu tempuh, rumusnya adalah $\!t=\frac{s}{v}$ .

3. Untuk mencari kecepatan, rumusnya adalah $\!v=\frac{s}{t}$ .

Gerak lurus berubah beraturan

Gerak lurus berubah beraturan adalah gerak yang lintasannya berupa garis lurus dengan kecepatannya yang berubah beraturan.

Percepatannya bernilai konstan/tetap.

Rumus GLBB ada 3, yaitu:

$\!v_{t}=\!v_{0}+\!a\times\!t$

$\!s=\!v_{0}\times\!t+\frac{1}{2}\times\!a\times\!t^2$

$\!v_{t}^2=\!v_{0}^2+\!2\times\!a\times\!s$

Dengan ketentuan:

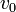$\!v_{0}$ = Kecepatan awal (m/s)
$\!v_{t}$ = Kecepatan akhir (m/s)
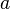$\!a$ = Percepatan (m/s²)
$\!s$ = Jarak yang ditempuh (m)

B. Gerak Parabola

Gerak parabola merupakan gerak dua dimensi suatu benda yang bergerak membentuk sudut elevasi dengan sumbu x atau sumbu y. Sumbu x (horizontal) merupakan GLB dan sumbu y (vertikal) merupakan GLBB. Kedua gerak ini tidak saling memengaruhi, hanya saja membentuk suatu gerak parabola.

Nama lainnya disebut juga dengan gerak peluru yang memiliki bentuk lintasan parabola. Lintasan parabola dapat diilustrasikan seperti pada gambar di bawah ini.

Ilustrasi lintasan

Pada gambar terlihat ada simbol x dan y, komponen-komponen di antaranya memiliki arah yang berbeda.

Komponen Sumbu X

Dalam gerak parabola, komponen sumbu x merupakan komponen GLB. GLB merupakan kecepatan di sumbu horizontal pada titik ataupun posisi tetap. Pada sumbu x, komponen awal ialah simbol dari kecepatan awal. Secara matematis, nilai didapatkan dengan persamaan di bawah ini:

Oke, sekarang coba perhatikan tabel yang menunjukkan gerak parabola pada sumbu x ini:

Komponen Sumbu Y

Jika sumbu x merupakan komponen GLB, sumbu y atau arah vertikal komponen gerak merupakan GLBB. Perbedaan sumbu x dengan sumbu y ialah simbol perpindahan/jarak pada sumbu x ditunjukkan dengan s, sedangkan pada sumbu y ditunjukkan dengan y. Sumbu y kecepatan awal disimbolkan dengan. Sehingga, dapat dirumuskan sebagai berikut:

Sumbu x untuk gerak parabola telah ditetapkan beberapa rumus di bawah ini:

Sementara sumbu y untuk gerak parabola berlaku persamaan GLBB:

Gerak vertikal ke atas menggunakan rumus sebagai berikut:

Setelah didapat kecepatan di sumbu x (Vx) dan kecepatan di sumbu y (Vy), kita dapat mencari nilai kecepatan totalnya (Vg), dengan menggunakan rumus resultan kecepatan sebagai berikut:

Keterangan:

Vox = kecepatan awal pada sumbu x (m/s)

Voy = kecepatan awal pada sumbu y (m/s)vx = kecepatan setelah waktu (t) tertentu pad sumbu (m/s)

Vy = kecepatan setelah waktu (t) tertentu pada sumbu y (m/s)

VR = kecepatan total (m/s)

x = kedudukan benda pada sumbu x (horizontal) (m)

y = kedudukan benda pada sumbu y (vertikal) (m)

t = waktu (s)

g = percepatan gravitasi (m/s)

θ = sudut elevasi (o)

Menentukan Waktu pada Titik Puncak (Ketinggian Maksimum) dan Waktu pada Ketinggian Semula

Ketinggian maksimum dicapai pada saat benda mencapai titik tertinggi pada sumbu y. Pada ketinggian maksimum, kecepatan benda di titik tersebut Ialah 0 (Vy = 0). Secara matematis, rumus menentukan waktu untuk ketinggian maksimum dituliskan sebagai berikut:

tp = (vosinθ)/g

Untuk kembali ke posisi semula (mencapai jarak maksimum) dari keadaan awal, rumus yang digunakan dikali 2 dari waktu untuk mencapai ketinggian maksimum. Secara matematis, rumus menentukan waktu untuk kembali ke posisi semula dituliskan sebagai berikut:

tT = 2 x tp = 2 x (vosinθ)/g

Menentukan Ketinggian Maksimum (hmax)

Dalam menentukan ketinggian maksimum, rumus yang digunakan ialah sebagai berikut:

hmax = (vo2sin2θ)/2g

Menentukan Jangkauan Maksimum (Xmax)

Selain ketinggian maksimum, kita juga dapat menghitung jangkauan maksimum. Jangkauan maksimum merupakan jarak maksimum yang dijangkau pada sumbu horizontal (Sumbu x). Jangkauan maksimum dirumuskan sebagai berikut:

Xmax = (2vo2sinθcosθ)/g

Keterangan:

g = percepatan gravitasi (m/s2)

θ = sudut elevasi (o)

Vo = kecepatan awal (m/s)

Xmax = jangkauan maksimum (m)

hmax = ketinggian maksimum (m)

tp = waktu mencapai titik puncak (s)

tt = waktu mencapai jarak maksimum (s)

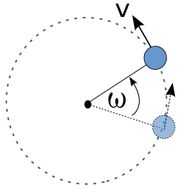
C. Gerak Melingkar

Gerak melingkar.

Gerak melingkar (atau gerak sirkuler; bahasa Inggris: circular motion) adalah gerak suatu benda yang membentuk lintasan berupa lingkaranmengelilingi suatu titik tetap. Agar suatu benda dapat bergerak melingkar ia membutuhkan adanya gaya yang selalu membelokkan-nya menuju pusat lintasan lingkaran. Gaya ini dinamakan gaya sentripetal. Suatu gerak melingkar beraturan dapat dikatakan sebagai suatu gerak dipercepat beraturan, mengingat perlu adanya suatu percepatan yang besarnya tetap dengan arah yang berubah, yang selalu mengubah arah gerak benda agar menempuh lintasan berbentuk lingkaran ^[1].

Ciri-ciri gerak melingkar beraturan:

1. Besar kelajuan linearnya tetap
2. Besar kecepatan sudutnya tetap
3. Besar percepatan sentripetalnya tetap
4. Lintasannya berupa lingkaran

Besaran gerak melingkar

Besaran-besaran yang mendeskripsikan suatu gerak melingkar adalah

\theta\!

,

\omega\!

dan

\alpha\!

atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan

r\!

,

v\!

dan

a\!

.

Besaran gerak lurus dan melingkar
Gerak lurus		Gerak melingkar
Besaran	Satuan (SI)	Satuan (SI)
posisi $r\!$	m	rad
kecepatan $v\!$	m/s	rad/s
percepatan $a\!$	m/s²	rad/s²
-	-	s
-	-	m

Turunan dan integral

Seperti halnya kembarannya dalam gerak linier, besaran-besaran gerak melingkar pun memiliki hubungan satu sama lain melalui proses integrasi dan diferensiasi.

\int \omega \ dt=\theta \quad \leftrightarrow \quad \omega ={\frac {d\theta }{dt}}

\int \alpha \ dt=\omega \quad \leftrightarrow \quad \alpha ={\frac {d\omega }{dt}}

\int \int \alpha \ dt^{2}=\theta \quad \leftrightarrow \quad \alpha ={\frac {d^{2}\theta }{dt^{2}}}

Hubungan antar besaran sudut dan tangensial

Antara besaran gerak linier dan melingkar terdapat suatu hubungan melalui

R\!

khusus untuk komponen tangensial, yaitu

\theta = \frac{r_T}{R}\ \ , \ \ \omega = \frac{v_T}{R}\ \ , \ \ \alpha = \frac{a_T}{R}

Perhatikan bahwa di sini digunakan

r_T\!

yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu

r_T \approx |\overrightarrow{r}(t+\Delta t)-\overrightarrow{r}(t)|\!

untuk suatu selang waktu kecil atau sudut yang sempit.

Jenis gerak melingkar

Gerak melingkar dapat dibedakan menjadi dua jenis, atas keseragaman kecepatan sudutnya

\omega\!

, yaitu:

gerak melingkar beraturan, dan
gerak melingkar berubah beraturan.

Gerak melingkar beraturan

Gerak Melingkar Beraturan (GMB) adalah gerak melingkar dengan besar kecepatan sudut

\omega\!

tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial

v_T\!

dengan jari-jari lintasan

R\!

.

\omega = \frac {v_T} R

Arah kecepatan linier

v\!

dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial

v_T\!

. Tetapnya nilai kecepatan

v_T\!

akibat konsekuensi dar tetapnya nilai

\omega\!

. Selain itu terdapat pula percepatan radial

a_R\!

yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.

a_R = \frac {v^2} R = \frac {v_T^2} R

Bila

T\!

adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran

\theta = 2\pi R\!

, maka dapat pula dituliskan

v_T = \frac {2\pi R} T \!

Kinematika gerak melingkar beraturan adalah

\theta(t) = \theta_0 + \omega\ t

dengan

\theta(t)\!

adalah sudut yang dilalui pada suatu saat

t\!

,

\theta_0\!

adalah sudut mula-mula dan

\omega\!

adalah kecepatan sudut (yang tetap nilainya).

Gerak melingkar berubah beraturan

Gerak Melingkar Berubah Beraturan (GMBB) adalah gerak melingkar dengan percepatan sudut

\alpha\!

tetap. Dalam gerak ini terdapat percepatan tangensial

a_T\!

(yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial

v_T\!

).

\alpha = \frac {a_T} R

Kinematika GMBB adalah

\omega(t) = \omega_0 + \alpha\ t \!

\theta(t) = \theta_0 + \omega_0\ t + \frac12 \alpha\ t^2 \!

\omega^2(t) = \omega_0^2 + 2 \alpha\ (\theta(t) - \theta_0) \!

dengan

\alpha\!

adalah percepatan sudut yang bernilai tetap dan

\omega_0\!

adalah kecepatan sudut mula-mula.

Persamaan parametrik

Gerak melingkar dapat pula dinyatakan dalam persamaan parametrik dengan terlebih dahulu mendefinisikan:

titik awal gerakan dilakukan $(x_0,y_0)\!$
kecepatan sudut putaran $\omega\!$ (yang berarti suatu GMB)
pusat lingkaran $(x_c,y_c)\!$

untuk kemudian dibuat persamaannya ^[2].

Hal pertama yang harus dilakukan adalah menghitung jari-jari lintasan

R\!

yang diperoleh melalui:

R = \sqrt{(x_0 - x_c)^2 + (y_0 - y_c)^2} \!

Setelah diperoleh nilai jari-jari lintasan, persamaan dapat segera dituliskan, yaitu

x(t)=x_{c}+R\cos(\omega t+\phi _{x})\!

y(t)=y_{c}+R\sin(\omega t+\phi _{y})\!

dengan dua konstanta

\phi_x \!

dan

\phi_y \!

yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai

(x_0,y_0)\!

, maka dapat ditentukan nilai

\phi_x \!

dan

\phi_y \!

:

\phi_x = \arccos \left( \frac{x_0 - x_c}{R} \right)\!

\phi_y = \arcsin \left( \frac{y_0 - y_c}{R} \right)\!

Perlu diketahui bahwa sebenarnya

\phi_x = \phi_y \!

karena merupakan sudut awal gerak melingkar.

Kecepatan sudut tidak tetap

Persamaan parametric dapat pula digunakan apabila gerak melingkar merupakan GMBB, atau bukan lagi GMB dengan terdapatnya kecepatan sudut yang berubah beraturan (atau adanya percepatan sudut). Langkah-langkah yang sama dapat dilakukan, akan tetapi perlu diingat bahwa

\omega \rightarrow \omega(t) = \int \alpha dt = \omega_0 + \alpha t \!

dengan

\alpha\!

percepatan sudut dan

\omega_0\!

kecepatan sudut mula-mula. Penurunan GMBB ini akan menjadi sedikit lebih rumit dibandingkan pada kasus GMB di atas.

Persamaan parametrik di atas, dapat dituliskan dalam bentuk yang lebih umum, yaitu:

x(t) = x_c + R \cos \theta \!

y(t) = y_c + R \sin \theta \!

di mana

\theta = \theta(t) \!

adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara

\theta \!

,

\omega \!

dan

\alpha \!

melalui proses integrasi dan diferensiasi, maka dalam kasus GMBB hubungan-hubungan tersebut mutlak diperlukan.

Kecepatan sudut

Dengan menggunakan aturan rantai dalam melakukan diferensiasi posisi dari persamaan parametrik terhadap waktu diperoleh

v_x(t) = - R \sin \theta\ \frac{d\theta}{dt} = - \omega(t) R \sin \theta \!

v_y(t) = R \cos \theta \ \frac{d\theta}{dt} = \omega(t) R \cos \theta \!

dengan

\frac{d\theta}{dt} = \omega(t) = \omega_0 + \alpha\ t \!

Dapat dibuktikan bahwa

v(t) = v_T(t) = \sqrt{v_x^2(t) + v_y^2(t)} = \omega(t) R \!

sama dengan kasus pada GMB.

Gerak berubah beraturan

Gerak melingkar dapat dipandang sebagai gerak berubah beraturan. Bedakan dengan gerak lurus berubah beraturan (GLBB). Konsep kecepatan yang berubah kadang hanya dipahami dalam perubahan besarnya, dalam gerak melingkar beraturan (GMB) besarnya kecepatan adalah tetap, akan tetapi arahnya yang berubah dengan beraturan, bandingkan dengan GLBB yang arahnya tetap akan tetapi besarnya kecepatan yang berubah beraturan.

Gerak berubah beraturan
Kecepatan	GLBB	GMB
Besar	berubah	tetap
Arah	tetap	berubah

[1]

[2]

[3]

[1]

[2]

Materi Fisika Kelas XI

By Andre Imanuel Sianturi

BTemplates.com

About

Sunday, September 9, 2018

VEKTOR,PARABOLA DAN GERAK MELINGKAR

Gerak – Pengantar

Vektor Satuan dan Vektor Posisi

Ukuran benda dapat diwakili oleh sebuah titik materi atau partikel. Posisi titik materi dinyatakan dengan sebuah vektor. Vektor ini dinyatakan dengan vektor-vektor satuan.

→Vektor Satuan

→Vektor Posisi

Vektor posisi adalah vektor yang menyatakan posisi suatu titik materi pada suatu bidang datar (dimensi dua) atau dalam ruang (dimensi tiga). Posisi suatu titik materi pada bidang datar atau dalam ruang dinyatakan oleh vektor posisi r .

Perpindahan

∆r = r2 – r1= (x2 – x1)i + (y2 – y1)j + (z2 – z1)k

Satuan kecepatan

Contoh berbagai kecepatan

Konsep Turunan (Diferensial) dan integral

Konsep Turunan dan integral pada vektor posisi, kecepatan dan percepatan

Definisi dan sifat-sifat

Percepatan rata-rata

Percepatan sesaat

Rumus GLB dan GLBB

Gerak lurus beraturan

Sistem koordinat kutub dua dimensi

Gerak Lurus Beraturan (GLB) adalah suatu gerak lurus yang mempunyai kecepatan konstan. Maka nilai percepatannya adalah a = 0. Gerakan GLB berbentuk linear dan nilai kecepatannya adalah hasil bagi jarak dengan waktu yang ditempuh.

Rumus:

Dengan ketentuan:

= Jarak yang ditempuh (km, m)

= Kecepatan (km/jam, m/s)

= Waktu tempuh (jam, sekon)

Catatan:

Untuk mencari jarak yang ditempuh, rumusnya adalah .

Untuk mencari waktu tempuh, rumusnya adalah .

3. Untuk mencari kecepatan, rumusnya adalah .

Gerak lurus berubah beraturan

Gerak lurus berubah beraturan adalah gerak yang lintasannya berupa garis lurus dengan kecepatannya yang berubah beraturan.

Percepatannya bernilai konstan/tetap.

Rumus GLBB ada 3, yaitu:

Dengan ketentuan:

= Kecepatan awal (m/s)

= Kecepatan akhir (m/s)

= Percepatan (m/s2)

= Jarak yang ditempuh (m)

Besaran gerak melingkar

Turunan dan integral

Hubungan antar besaran sudut dan tangensial

Jenis gerak melingkar

Gerak melingkar beraturan

Gerak melingkar berubah beraturan

Persamaan parametrik

Kecepatan sudut tidak tetap

Kecepatan sudut

Gerak berubah beraturan

..

Popular Posts

Blog Archive

About

Blogroll

$\!s$ = Jarak yang ditempuh (km, m)

$\!v$ = Kecepatan (km/jam, m/s)

$\!t$ = Waktu tempuh (jam, sekon)

Untuk mencari jarak yang ditempuh, rumusnya adalah $\!s=\!v\times\!t$ .

Untuk mencari waktu tempuh, rumusnya adalah $\!t=\frac{s}{v}$ .

3. Untuk mencari kecepatan, rumusnya adalah $\!v=\frac{s}{t}$ .

$\!v_{0}$ = Kecepatan awal (m/s)

$\!v_{t}$ = Kecepatan akhir (m/s)

$\!a$ = Percepatan (m/s²)

$\!s$ = Jarak yang ditempuh (m)